Zeno's Paradox of Motion

This is a famous paradox that tries to prove that motion is impossible. In the form presented, it is actually an infinite class of paradoxes branching on premise (2) as their subconclusion. We will not resolve the infinite class, but instead lay to rest two popular arguments within the class.

Infinite Time Subargument

Here, premise (2) is not true. It may be expanded as a subargument making its own infinite class of arguments, but this time it is easier to notice that time converges to a finite value just as distance does because the time it takes to traverse each interval is proportional to the length of the interval: Say t=time for interval, l=interval length, L=total distance. Then t=kl for some constant k. Sum[t]=Sum[kl]=k*Sum[l]=k*L which is finite.

Infinite Tasks Subargument

In this case, we have run into a problem with the definition of the word "task". When definition confusion ocurrs, the choice of which meaning to preserve is arbitrary. In order to make the most convenient choice, we consider the meanings of the word "task". In this case, the "task" referred to in the current subargument about Achilles is a special type of task that we will call a "continuous-task", and the "task" referred to in the Thomson's Lamp argument is another type of task that we will call a "discrete-task".

Premise (2) will be discredited using Leibnitz's Law to prove that discrete-tasks are different than continuous tasks. When this has been done, it will be conceivable that it is impossible to perform infinitely many discrete-tasks, while it is still possible to perform infinitely many continuous tasks. This may at first sound strange due to the fact that both are a type of task, but in general, sets do not share all the properties of their subsets, and so a property of discrete-tasks cannot be used to prove something about tasks unless the property is also shown to be a property of tasks.

The property that a continuous-task has that a general task does not is the following: as the time taken for the task goes to zero, the quantity of change to the state of the universe goes to zero. A discete-task has the property that it does not satisfy this requirement, so both type are different than tasks in general and different from each other by Leibnitz's Law. As a side note, discrete-tasks and continuous-tasks, form a partition of all tasks so that any tasks can be classified as one or the other. 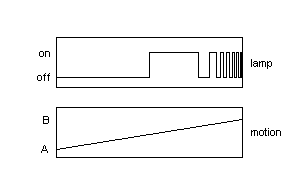Switching Thomson's Lamp is a discrete-task because no matter how fast the switch is flipped, it always causes the same change in the state of the universe; we could say that the number of lamps turned on changes by 1. Traversing an interval is a continuous-task because if you look at a short enough interval of time, you can force the distance traversed to be smaller than any given value (this of course assumes a finite velocity). To illustrate this concept better, we may create task-functions to represent the state of the universe versus time. The task-functions for the lamp and motion are below:
The lamp's funtion has an oscillating discontinuity, but the motion's function is continuous everywhere. This is because the above-mentioned criteria for continuous-tasks is the same as the criteria for its task-function to be continuous (lim_h-> 0 f(t+h)=f(t) <=> lim_h-> 0 f(t+h)-f(t)=0 <=> change goes to zero as time elapsed goes to 0 ).

It may be unclear why a continuous task function is the criteria used to distinguish between the uses of "task" in the two arguments. Rest assured, this property is not an arbitrary choice that arises from coincidence; it is the cause of the incompatibility of the arguments. The reason for this is that infinity is a purely conceptual thing; nothing in the real world can ever be infinite. We may pretend that there are infinitely many intervals between two points, but these correspond only to imagined intervals and not physical objects. Therefore, we must be careful to isolate all uses of the concept of infinity so that they effectively cancel out before they impose any real world consequences. When a lamp is switched infinitely many times, there is nothing to cancel out the infinity, so there is actually an infinite process ocurring in reality. On the other hand, when infinitely many intervals are traversed, the only reason why this is happening is because we imagine that there actually are infinitely many intervals. It is just as plausible that there are only N intervals, and N are being traversed, as in the case if space is quantized, or even that there is just 1 interval. This is intended to show that the infinitude of intervals that we picture has no impact on the laws of the universe, so the infinity is effectively isolated. So, a continuous task function basically allows the change to be split into an infinite sum without causing the result to be infinite (This can be illustrated better mathematically if the task-functions are made non-decreasing so that the lamp's function flies off to infinite at the end). This particular argument of Zeno's Paradox has been resolved, though it remains to be shown that all subarguments are unsound.